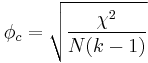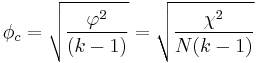Cramér's V

Cramér's V (φc)

In statistics, Cramér's V (sometimes referred to as Cramér's phi and denoted as φ_c) is a popular measure of association between two nominal variables, giving a value between 0 and +1 (inclusive). It is based on Pearson's chi-squared statistic and was published by Harald Cramér in 1946^[1]

Contents 1 Usage and interpretation 2 Calculation 3 See also 4 References 5 External links

Usage and interpretation

φ_c is the intercorrelation of two discrete variables^[2] and may be used with variables having two or more levels. φ_c is a symmetrical measure, it does not matter which variable we place in the columns and which in the rows. Also, the order of rows/columns doesn't matter, so φ_c may be used with nominal data types or higher (ordered, numerical, etc)

Cramér's V may also be applied to goodness of fit chi-squared models when there is a 1×k table (e.g: r=1). In this case k is taken as the number of optional outcomes and it functions as a measure of tendency towards a single outcome.

Cramér's V varies from 0 (corresponding to no association between the variables) to 1 (complete association) and can reach 1 only when the two variables are equal to each other.

φ_c² is the mean square canonical correlation between the variables.

In the case of a 2×2 contingency table Cramér's V is equal to the Phi coefficient.

Note that as chi-squared values tend to increase with the number of cells, the greater the difference between r (rows) and c (columns), the more likely φ_c will tend to 1 without strong evidence of a meaningful correlation.

Calculation

Cramér's V is computed by taking the square root of the chi-squared statistic divided by the sample size and the length of the minimum dimension (k is the smaller of the number of rows r or columns c).

The formula for the φ_c coefficient is:

  

where:

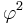• is the phi coefficient.
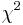• is derived from Pearson's chi-squared test
• is the grand total of observations and
• being the number of rows or the number of columns, whichever is less.

The p-value for the significance of φ_c is the same one that is calculated using the Pearson's chi-squared test .

The formula for the variance of φ_c is known^[3].

See also

Other measures of correlation for nominal data:

• The phi coefficient
• Tschuprow's T
• The uncertainty coefficient
• The Lambda coefficient

Other related articles:

• Contingency table
• Effect size

References

• Cramér, H. (1999). Mathematical Methods of Statistics, Princeton University Press

External links

• A Measure of Association for Nonparametric Statistics (Alan C. Acock and Gordon R. Stavig Page 1381 of 1381–1386)
• Nominal Association: Phi, Contingency Coefficient, Tschuprow's T, Cramer's V, Lambda, Uncertainty Coefficient

Statistics   Descriptive statistics Continuous data Location Mean (Arithmetic, Geometric, Harmonic) Median Mode Dispersion Range Standard deviation Coefficient of variation Percentile Interquartile range Shape Variance Skewness Kurtosis Moments L-moments Count data Index of dispersion Summary tables Grouped data Frequency distribution Contingency table Dependence Pearson product-moment correlation Rank correlation (Spearman's rho, Kendall's tau) Partial correlation Scatter plot Statistical graphics Bar chart Biplot Box plot Control chart Correlogram Forest plot Histogram Q-Q plot Run chart Scatter plot Stemplot Radar chart   Data collection Designing studies Effect size Standard error Statistical power Sample size determination Survey methodology Sampling Stratified sampling Opinion poll Questionnaire Controlled experiment Design of experiments Randomized experiment Random assignment Replication Blocking Factorial experiment Optimal design Uncontrolled studies Natural experiment Quasi-experiment Observational study   Statistical inference Statistical theory Sampling distribution Sufficient statistic Meta-analysis Bayesian inference Bayesian probability Prior Posterior Credible interval Bayes factor Bayesian estimator Maximum posterior estimator Frequentist inference Confidence interval Hypothesis testing Likelihood-ratio Specific tests Z-test (normal) Student's t-test F-test Pearson's chi-squared test Wald test Mann–Whitney U Shapiro–Wilk Signed-rank Kolmogorov–Smirnov test General estimation Bias Robustness Efficiency Maximum likelihood Method of moments Minimum distance Density estimation   Correlation and regression analysis Correlation Pearson product-moment correlation Partial correlation Confounding variable Coefficient of determination Regression analysis Errors and residuals Regression model validation Mixed effects models Simultaneous equations models Linear regression Simple linear regression Ordinary least squares General linear model Bayesian regression Non-standard predictors Nonlinear regression Nonparametric Semiparametric Isotonic Robust Generalized linear model Exponential families Logistic (Bernoulli) Binomial Poisson Partition of variance Analysis of variance (ANOVA) Analysis of covariance Multivariate ANOVA Degrees of freedom   Categorical, multivariate, time-series, or survival analysis Categorical data Cohen's kappa Contingency table Graphical model Log-linear model McNemar's test Multivariate statistics Multivariate regression Principal components Factor analysis Cluster analysis Copulas Time series analysis Decomposition (Trend, Stationary process) ARMA model ARIMA model Vector autoregression Spectral density estimation Survival analysis Survival function Kaplan–Meier Logrank test Failure rate Proportional hazards models Accelerated failure time model   Applications Biostatistics Bioinformatics Biometrics Clinical trials & studies Epidemiology Medical statistics Engineering statistics Chemometrics Methods engineering Probabilistic design Process & Quality control Reliability System identification Social statistics Actuarial science Census Crime statistics Demography Econometrics National accounts Official statistics Population Psychometrics Spatial statistics Cartography Environmental statistics Geographic information system Geostatistics Kriging Category Portal Outline Index